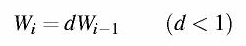Consideriamo che la dimensione delle code nel sistema sia un indice del carico a cui il sistema stesso è sottoposto (consideraimo sempre il sistema composto da due processi e dalla linea che li connette).
Nel caso di un sistema in equilibrio, possiamo considerare che il carico resti costante, e possa dunque essere espresso, per ogni intervallo di campionamento i, da:
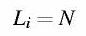
In caso di congestione, invece, del carico bisogna considerare almeno una componente di ordine superiore (à la Taylor):
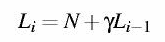
dove il fattore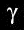 
(maggiore di uno in congestione)
indica il traffico che rimane inevaso dal precedente
intervallo di campionamento.
E' facile vedere che il carico tende così a crescere esponenzialmente. Una soluzione per la precedente equazione differenziale, nelle stesse condizioni, è:
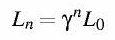
Per correggere una divergenza esponenziale serve uno smorzamento pure esponenziale. Quindi la finestra dovrà decrescere in modo esponenziale:
next: Allargamento dinamico della finestra.
previous: Riduzione dinamica della finestra.
up: La congestione nelle reti di comuicazione
