Rappresentazione binaria

Per informazione intendiamo tutto quello che viene manipolato da un calcolatore:

  • Numeri (naturali, interi, reali,...)
  • Caratteri
  • Immagini
  • Suoni
  • Programmi

La più piccola unità di informazione memorizzabile o elaborabile da un calcolatore, il bit, corrisponde allo stato di un dispositivo fisico che viene interpretato come 0 o1.

In un calcolatore tutte le informazioni sono rappresentate in forma binaria, come sequenze di 0 e 1.

Per motivi tecnologici: distinguere tra due valori di una grandezza fisica è più semplice che non ad esempio tra dieci valori (e pensare che l'ENIAC aveva 10 valvole per rappresentare una singola cifra nell'intervallo 0-9... mentre le combinazioni acceso/spento di 10 valvole sono 210 = 1024)


Rappresentazione posizionale

Un numero naturale è un oggetto matematico, che può essere rappresentato mediante una sequenza di simboli di un alfabeto fissato.

È importante distinguere tra un numero e la sua rappresentazione: la sequenza di cifre 234 è la rappresentazione decimale del numero 234. Così come la sequenza di cifre romane CCXXXIV è un'altra rappresentazione del numero 234.

Si distinguono 2 tipi di rappresentazione:

  • Additiva: ad esempio le cifre romane
  • Posizionale: una cifra contribuisce con un valore diverso al numero a seconda della posizione in cui si trova

Noi consideriamo solo la rappresentazione posizionale.

Nella sequenza di cifre:

cn-1 cn-2...c1 c0
  • c0 viene detta cifra meno significativa
  • cn-1 viene detta cifra più significativa


Rappresentazione di numeri naturali

Il numero b di cifre diverse (dimensione dell'alfabeto) è detto base del sistema di numerazione. Ad ogni cifra è associato un valore compreso tra 0 e b-1.

Base Alfabeto Sistema
2 0,1 binario
8 0,...,7 ottale
10 0,...,9 decimale
16 0,...,9,A,...,F esadecimale

Il significato di una sequenza di cifre (il numero N che essa rappresenta) dipende da b:

cn-1· bn-1+ cn-2· bn-2+...+c1· b1+ c0· b0 = N
Il numerale 101 rappresenta numeri diversi a seconda del sistema usato:

Sistema Base b (101)b Valore (in decimale)
binario 2 (101)2 1 · 22 + 0 · 21 + 1 · 20 = 5
ottale 8 (101)8 1 · 82 + 0 · 81 + 1 · 80 = 65
decimale 10 (101)10 1 · 102 + 0 · 101 + 1 · 100 = 101
esadecimale 16 (101)16 1 · 162 + 0 · 161 + 1 · 160 = 257


Intervallo di rappresentazione

Intervallo di rappresentazione: con n cifre in base b possiamo rappresentare bn valori, da 0 a bn-1. Esempio:
3 cifre in base 10: da 0 a 999 = 103-1
8 cifre in base 2 (1 byte): da 0 a 255 = 28-1
16 cifre in base 2 (2 byte): da 0 a 65.535 = 216-1
32 cifre in base 2 (4 byte): da 0 a 4.294.967.295 = 232-1

N.B. Più bit a disposizione per la rappresentazione di un numero corrisponde ad una maggiore ampiezza dell'intervallo di rappresentazione da 0 a bn-1


Conversione dalla base 10

Le cifre vengono determinate dalla meno significativa a quella più significativa. Esempio: (25)10=(????)2
N : b Quoziente Resto Cifra
25:2 12 1 c0
12:2 6 0 c1
6:2 3 0 c2
3:2 1 1 c3
1:2 0 1 c4
quindi (25) 10 = (11001)2

N.B. servono almeno 5 bit (con cui possiamo rappresentare i numeri da 0 a 31)


Rappresentazione di numeri interi

Nella rappresentazione vista abbiamo considerato solo numeri senza segno

Quando si considerano valori interi, per rappresentare il segno si può pensare di usare uno dei bit (quello più significativo) Questa convenzione viene detta rappresentazione tramite modulo e segno

  • Il bit più significativo (cn-1) rappresenta il segno
  • le altre n-1 cifre (cn-2...c0) rappresentano il valore assoluto
Supponiamo di considerare 4 cifre per la rappresentazione degli interi. Poiché una cifra si usa per rappresentare il segno, l'intervallo di rappresentazione è (-23,+23) che si rappresenta nel seguente modo:

Problemi:
  • doppia rappresentazione per lo zero (00...00 e 10...00)
  • le operazioni aritmetiche sono complicate (analisi per casi)
Per questi motivi, invece della rappresentazione tramite modulo e segno si usa una rappresentazione in complemento.

Rappresentazione in complemento a 2

Con base 2 e n cifre, abbiamo a disposizione 2n configurazioni distinte. Utilizziamo metà di tali configurazioni per rappresentare numeri positivi e l'altra metà per rappresentare numeri negativi ma in modo diverso rispetto alla rappresentazione in modulo e segno.

In particolare se N è

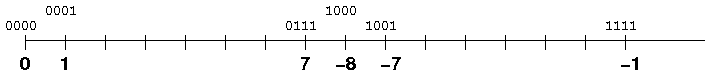
  • un numero non negativo minore di +2n-1 rappresento N in base 2
  • altrimenti rappresento 2n-N in base 2

In questo modo si rappresentano gli interi relativi nell'intervallo [-2n-1,+2n-1)

Come nella rappresentazione modulo e segno:

  • Positivi: cifra più significativa è 0 (rappresentati nella parte inferiore dell'intervallo)
  • Negativi: cifra più significativa è 1 (rappresentati nella parte superiore dell'intervallo)
Vantaggi (della rappresentazione in complemento):
  • Lo 0 ha una sola rappresentazione
  • La somma si effettua bit a bit
    • Esempio: n=5, intervallo di rappresentazione: da -24 a 24-1 (ovvero, da -16 a 15) 
      

     00011          00111           11111          01000

 +9   01001+    -9   10111+     -9   10111+    +9   01001+

 +3   00011=    +3   00011=     +9   01001=    +8   01000=
------------   ------------    ------------   ------------
+12   01100     -6   11010       0   00000     -15  10001
  • Non è necessario preoccuparsi dei segni
  • Il risultato sarà corretto (in complemento a 2 se negativo) a meno di trabocco (overflow).
N.B. Così come nel caso della rappresentazione dei numeri naturali senza segno anche per gli interi più bit a disposizione corrispondono ad una maggiore ampiezza dell'intervallo di rappresentazione da [-2n-1,+2n-1)

L'aritmetica reale
Anche in un intervallo chiuso, l'insieme dei reali (e dei razionali) è infinito: non è possibile rappresentare tutti i possibili valori di un certo intervallo

Rappresentazione in virgola fissa:

  • Si rappresentano separatamente, usando un numero fissato di cifre la parte intera e la parte frazionaria
Rappresentazione in virgola mobile:
  • Utilizza la notazione esponenziale. Si esprime il numero come prodotto di due parti:
    m · 2e = N
    Esempio: 0,75=(0,11)2=(0,11)2 · 20 ma anche (110)2 · 2-3
  • Si usa la rappresentazione in forma normalizzata in base 2
    • e è l'esponente in base 2: intero relativo
    • m è la mantissa in base 2: numero frazionario tale che
      ½   ≤   |m|   <   1
    Esempio: 0,75=(0,11)2 · 20

Rappresentazione in virgola mobile
Fissati:
  • k bit per la mantissa
  • h bit per l'esponente
  • 1 bit per il segno
l' insieme di reali rappresentabili è fissato (e limitato)
½   ≤   |m|   ≤   0.11...1
-2h-1   ≤   e   ≤   2h-1-1
Questo fissa anche massimo e minimo (in valore assoluto) numero rappresentabile.

Rappresentabilità in virgola mobile
Indichiamo con F l'insieme dei numeri rappresentabili in virgola mobile
  • Sottoinsieme finito dei numeri razionali rappresentabili (con n bit)
  • Simmetrico rispetto allo 0
  • Gli elementi non sono uniformemente distribuiti sull'asse reale
    • densi intorno allo 0, radi intorno al massimo rappresentabile:

      Esempio: Supponiamo k=3 e h=3

      m \ e -4 -3 -2 -1 0 1 2 3
      0,100 0.03125 0.0625 0.125 0.25 0.5 1 2 4
      0,101 0.0390625 0.078125 0.15625 0.3125 0.625 1.25 2.5 5
      0,110 0.046875 0.09375 0.1875 0.375 0.75 1.5 3 6
      0,111 0.0546875 0.109375 0.21875 0.4375 0.875 1.75 3.5 7

  • Molti razionali non appartengono ad F (ed esempio 1/3, 1/5,...)
  • Non è chiuso rispetto ad addizioni e moltiplicazioni
  • Per rappresentare un reale N si sceglie l'elemento di F più vicino ad N
  • La funzione che associa ad un reale N l'elemento di F più vicino è detta funzione di arrotondamento

Limitazioni aritmetiche dovute al fatto che il numero di bit usati per rappresentare un numero è limitato:

  • Perdita di precisione
  • Arrotondamento: mantissa non è sufficiente a rappresentare tutte le cifre significative del numero
  • Errore di overflow: esponente non è sufficiente (numero troppo grande)
  • Errore di underflow: numero troppo piccolo viene rappresentato come 0

Esempio: nello Standard IEEE 754 a 32 bit:

  • 1 bit per il segno della mantissa (0 positivo, 1 negativo)
  • 7 bit per l'esponente (in eccesso 127, l'esponente con tutti 0 è il più piccolo)
  • 24 bit per la mantissa (bit a 1 implicito a sinistra della virgola)
  • sia numeri normalizzati che denormalizzati (quando l'esponente ha tutti 0)
  • alcune configurazioni riservate (0, Not-a-Number, overflow)