Esercizi di modellizzazione
Esercizio n. 1.1.1
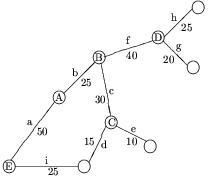
Una societa' di soccorso stradale ottiene in gestione il servizio
di assistenza sulla rete autostradale riportata nel grafo in figura,
dove i nodi rappresentano le uscite, gli archi le singole tratte
e i numeri sugli archi le lunghezze delle tratte. La societa' ha la
possibilita' di aprire un centro di assistenza nei pressi delle uscite
A, B, C, D ed E con costo cA, cB, cC, cD e cE rispettivamente.
Per garantire la voluta rapidita' di intervento, ciascun
punto della rete autostradale deve distare al massimo 50 km dal centro
di assistenza piu' vicino; inoltre, per esigenze amministrative ciascun
centro deve garantire l'assistenza su tratte intere e non su sue parti.
Formulare il problema della scelta dei centri di assistenza da aprire
in modo che il servizio sia garantito su tutta la rete ed il costo di
istallazione dei centri sia minimo.
Esercizio n. 1.1.2
Formulare lo stesso problema dell' esercizio 1.1.1 con l' ulteriore vincolo
che ciascun centro possa effettuare il servizio di assistenza solo per tratte
autostradali di lunghezzza complessiva non superiore a 80 Km.
Esercizio n. 1.1.3
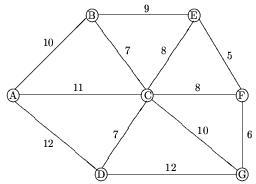
Una societa' di telecomunicazioni vuole dislocare il maggior numero
possibile di ripetitori nelle localita' individuate dai nodi del
grafo in figura senza che possano esserci interferenze; i numeri sugli
archi rappresentano la distanza chilometrica tra localita' adiacenti.
Sapendo che il raggio di azione di ciascun ripetitore e' di 5 km,
formulare il problema.
Esercizio n. 1.1.4
Un' industria deve produrre la collezione primavera-estate del noto
stilista Armadi. Per questo deve acquistare rotoli di tessuto, che
hanno una lunghezza fissata ma sono disponibili in n diverse larghezze
a(1) < a(2) < ... < a(n) con costo C(1) < C(2) < ... < C(n).
Ogni capo deve essere tessuto da una pezza di almeno una data
larghezza: la ditta conosce il numero D(i) di rotoli di larghezza a(i)
necessario a produrre tutti i capi di larghezza al piu' a(i) e maggiore di
a(i-1). Ovviamente ogni capo di vestiario che puo' essere tagliato
utilizzando una pezza di larghezza a(i) puo' essere tagliato da una
pezza di larghezza a(j) con j > i. L' industria deve pero' noleggiare
i complessi macchinari a controllo numerico che sono necessari per
tagliare il tessuto: ciascun macchinario puo' tagliare solo da rotoli
di una data larghezza a(i) ed ha un costo di noleggio K(i). Si formuli
il problema di decidere quali macchinari noleggiare, e conseguentemente
anche quanti rotoli di ciascuna larghezza acquistare, per minimizzare
il costo complessivo dato dalla somma del costo di noleggio dei
macchinari e il costo dei rotoli acquistati.
Suggerimento: il problema puo' essere formulato come un problema di
cammino minimo.
Esercizio n. 1.1.5
L' Elimagna deve programmare la produzione di panettoni per il prossimo
anno. L' ufficio vendite ha fornito le previsioni di vendita mensili:
d(i) e' il numero di panettoni richiesti nel mese i. Sono noti il
costo unitario di produzione, c, ed il costo unitario mensile di
magazzino, p. C' e' anche un costo fisso di "set up" dell' impianto,
s: infatti, se si decide in un dato mese di produrre panettoni,
bisogna preparare la linea di produzione e questo comporta un costo
indipendente dal numero di panettoni prodotto. Assumiamo che i
panettoni vengano prodotti ed immagazzinati o consegnati ai
distributori alla fine di ogni mese. La capacita' di immagazzinamento
nel mese i e' m(i). Sapendo che all' inizio dell' anno il magazzino
non contiene panettoni e lo stesso deve avvenire alla fine dell' anno,
formulare come problema di Programmazione Matematica il problema della
determinazione del piano di produzione di costo minimo.
Esercizio n. 1.1.6
Dipartimento di Informatica intende assegnare n diversi lavori di
preparazione di pagine web a m (m < n) cooperative di studenti di
Informatica. La cooperativa j, per effettuare il lavoro i, richiede
al Dipartimento un pagamento di c(i,j) Euro. Inoltre, per ragioni di
riservatezza, per ogni lavoro i si conosce l'insieme C(i) dei lavori
che possono essere effettuati assieme ad i dalla stessa cooperativa.
Il Dipartimento intende assegnare i lavori delle pagine web alle
cooperative al minimo costo con la garanzia di assegnare almeno un
lavoro ad ogni cooperativa e facendo si' che alla stessa cooperativa
siano assegnati solo lavori compatibili.
Formulare in termini di P.L.I. il problema del Dipartimento.
Esercizio n. 1.1.7
Un impresario edile decide di costruire un villaggio residenziale
composto da n palazzine, la cui altezza puo' essere h(1), h(2), .... , h(k).
Il costo di costruzione di una palazzina dipende dalla sua altezza: vale c(j)
nel caso di una palazzina di altezza h(j). In base alle normative urbanistiche
vigenti, il dislivello tra la palazzina piu' alta e quella piu' bassa non deve
eccedere una soglia data. Sapendo che la palazzina i, se costruita di altezza h(j),
potra' ospitare a(i,j) famiglie, si formuli in termini di P.L.I. il
problema di costruire a costo minimo il quartiere in modo che esso sia
in grado di ospitare almeno d famiglie.
Esercizio n. 1.1.8
Una società può produrre un bene da immettere sul mercato.
Nel caso in cui decida di produrlo dovrà sostenere un costo
iniziale pari a c0 di avvio produzione. Fino a una quantità h1 il
prodotto ha un costo di produzione unitario pari a c1, successivamente
la società può produrre ulteriori quantità a un costo unitario pari
a c2>c1 fino ad una produzione totale massima h2.
Il prodotto può essere venduto a un prezzo unitario pari ad a1 fino
a una quantità massima u1, mentre ulteriori vendite possono
avvenire solo a un prezzo unitario a2 inferiore ad a1.
Esprimere costi e ricavi mediante funzioni lineari.
Formulare il problema di decidere quale quantità produrre per
massimizzare la differenza fra ricavi e costi, supponendo che tutta la
quantità di bene prodotta sia venduta.


